
Self-contained calculator, with flexibility to vary the number of treatments With post-hoc Tukey HSD has to be done manually, if you know how to! This Within Excel, followup of a successful ANOVA Microsoft Excel can do one-way ANOVA of multiple treatments (columns) nicely.īut it stops there in its tracks. Is equivalent to a t-test with the \(F\) ratio such that \(F=t^2\). Multiple treatments/ samples is not conducted. Samples to be compared, so the Tukey HSD Test for pairwise comparison of *Note that when \(k=2\) there is only one pair of (independent) treatements/ To continue with the next step of data entry. Treatments, and subsequently click the box below to enter your treatment data ↑ Uncheck the above box and select your appropriate \(k=\) number of You may, of course, overwrite the demo example data, but \(k=4\) would remainįixed in the demo irrespective of your selection of \(k\).
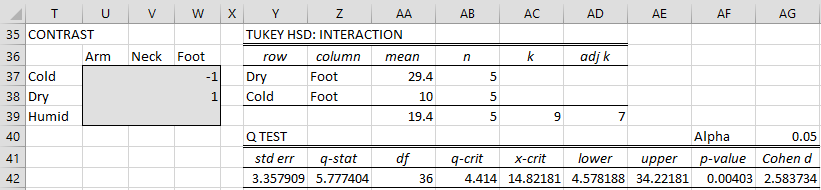
This box if you wish to use the demo example data with \(k=4\) treatments. Maximum of 10 treatments, which is more than adequate for most researchers. This would lead to an input screen with \(k\) columns to paste your Of observations of each treatment may be different. Since these are independent and not paired or correlated, the number Select \(k\), the number of independent treatments, sometimes also called unbalanced observations) - Select the number of treatments, then enter your observation data by typing or copy-paste, then proceed to the results Select the number of independent treatments below: Tukey HSD uses with Tukey-Kramer formula when treatments (sample groups) have unequal observations (i.e. One-way Anova with post-hoc Tukey HSD Calculator, with Scheffé,īonferroni and Holm multiple comparson results also provided. now mooooooved to the above domain name ! Significant Difference) Test Calculator for comparing multiple treatments. # C - B = 0 -0.02825 1.18744 -0.024 0.One-way ANOVA (ANalysis Of VAriance) with post-hoc Tukey HSD (Honestly # Pairwise comparisons using t tests with pooled SD pairwise.t.test(Y, Group, p.thod = "none") Likewise, it appears that the results of emmeans with no adjustment and those of glht with no adjustment, will match those of pairwise.t.test with no adjustment. # (Adjusted p values reported - single-step method) # Simultaneous Tests for General Linear Hypotheses Summary(mc, test=adjusted("single-step"))
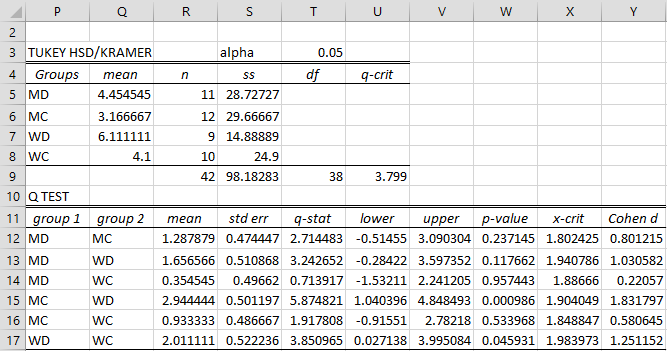
# P value adjustment: tukey method for comparing a family of 3 estimates. # contrast estimate SE df t.ratio p.value See also the example on RPubs.Īt least for the simple case of a one-way design with equal variances in groups (but potentially unequal sample sizes), it appears that the results of TukeyHSD will match those of emmeans with a Tukey adjustment, and those of glht with a "single-step" adjustment.
TUKEY KRAMER NUMBER LINE CODE
The code for the function can be found on GitHub. By default, ghlt uses a "single-step" correction method, but other correction methods could be used.Īs far as I can tell, the TukeyHSD function uses the Tukey-Kramer procedure. It just means "do all pairwise comparisons". In glht, "tukey" doesn't refer to Tukey's HSD.


 0 kommentar(er)
0 kommentar(er)
